Numbers
The decimal numerals themselves have no real meaning. After all, what is "the number 5?" Has anyone ever seen, heard or touched a "number 5?"  No, of course not! The number 5 like all numerals and combinations thereof, is an abstraction; an idea or construction, used to represent something else. Mathematics is the study of abstractions and their relations, and the counting numbers just described are the first abstraction we have learned about.
No, of course not! The number 5 like all numerals and combinations thereof, is an abstraction; an idea or construction, used to represent something else. Mathematics is the study of abstractions and their relations, and the counting numbers just described are the first abstraction we have learned about.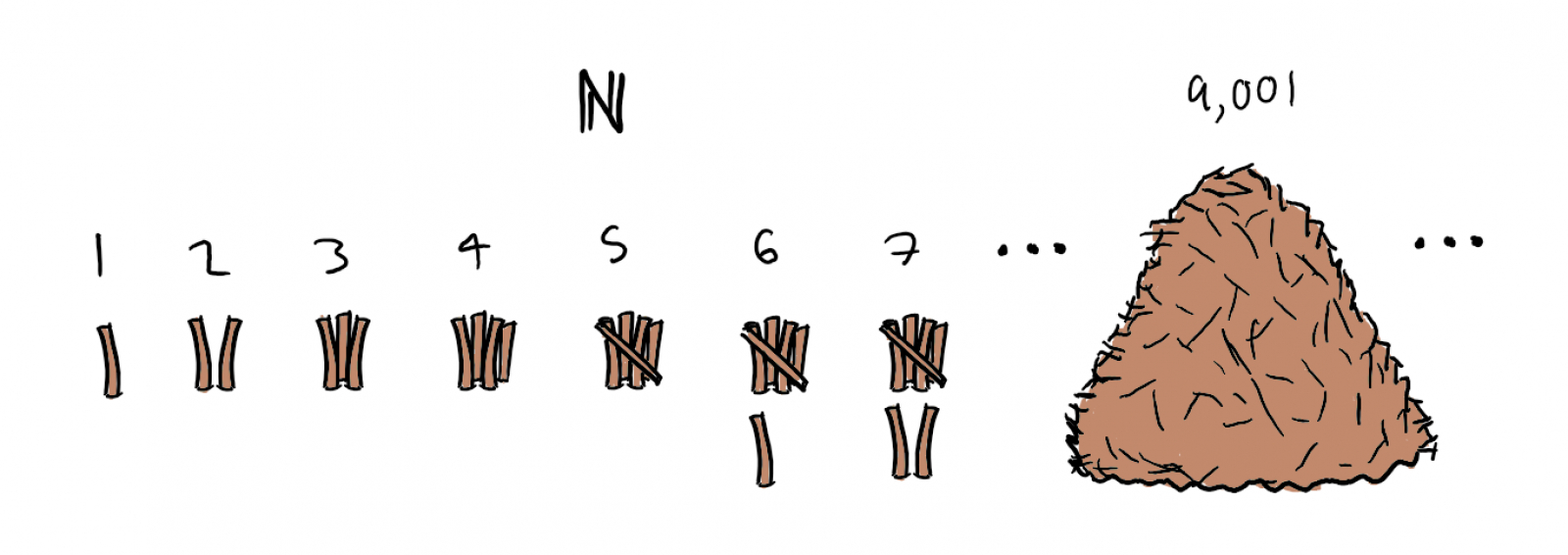 The natural numbers are represented symbolically, with a double-stroke letter, N.
The natural numbers are represented symbolically, with a double-stroke letter, N.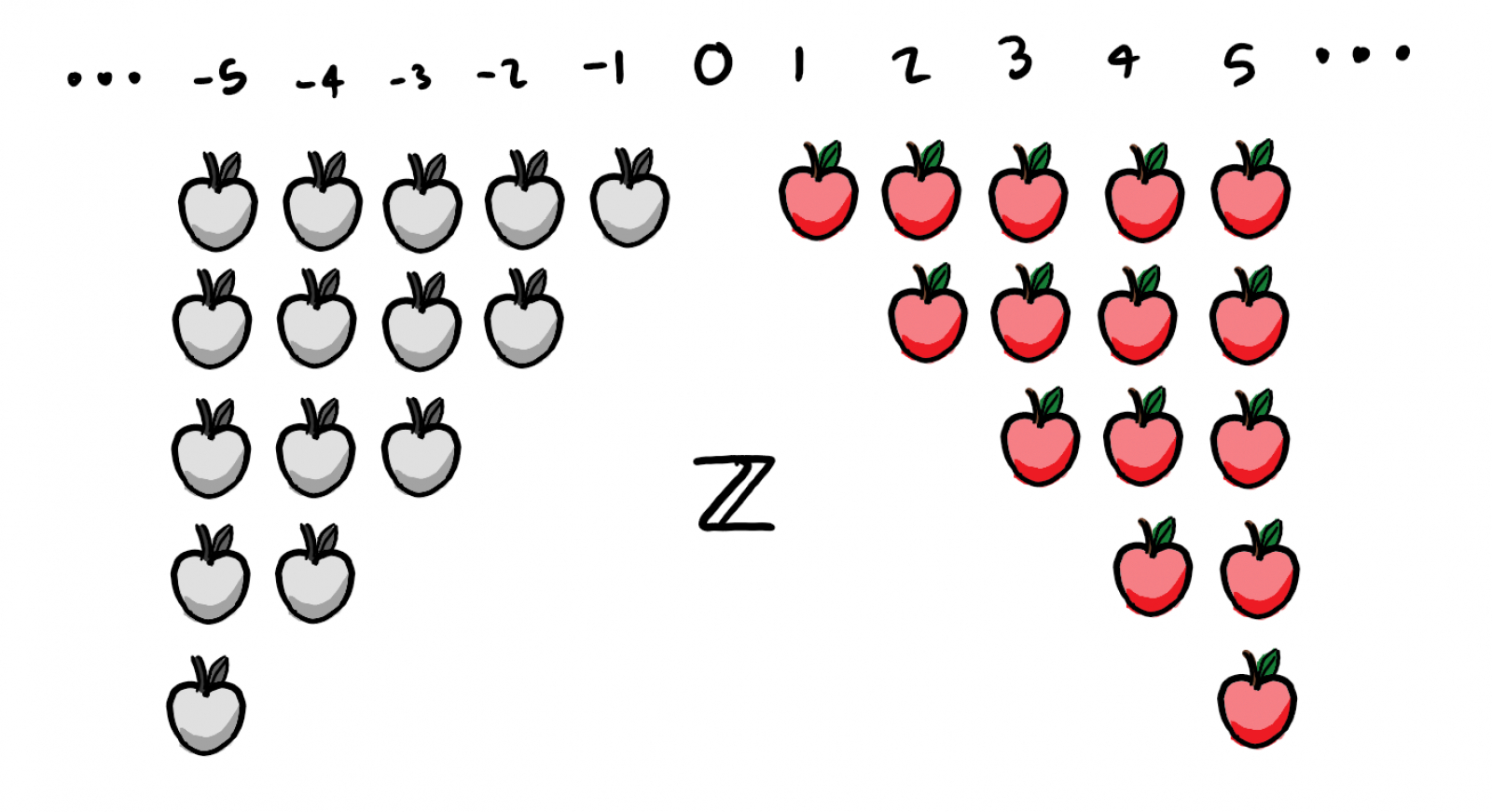 This idea of a number system containing both zero and negative numbers is known as the integers, and they are represented with the letter Z.
This idea of a number system containing both zero and negative numbers is known as the integers, and they are represented with the letter Z.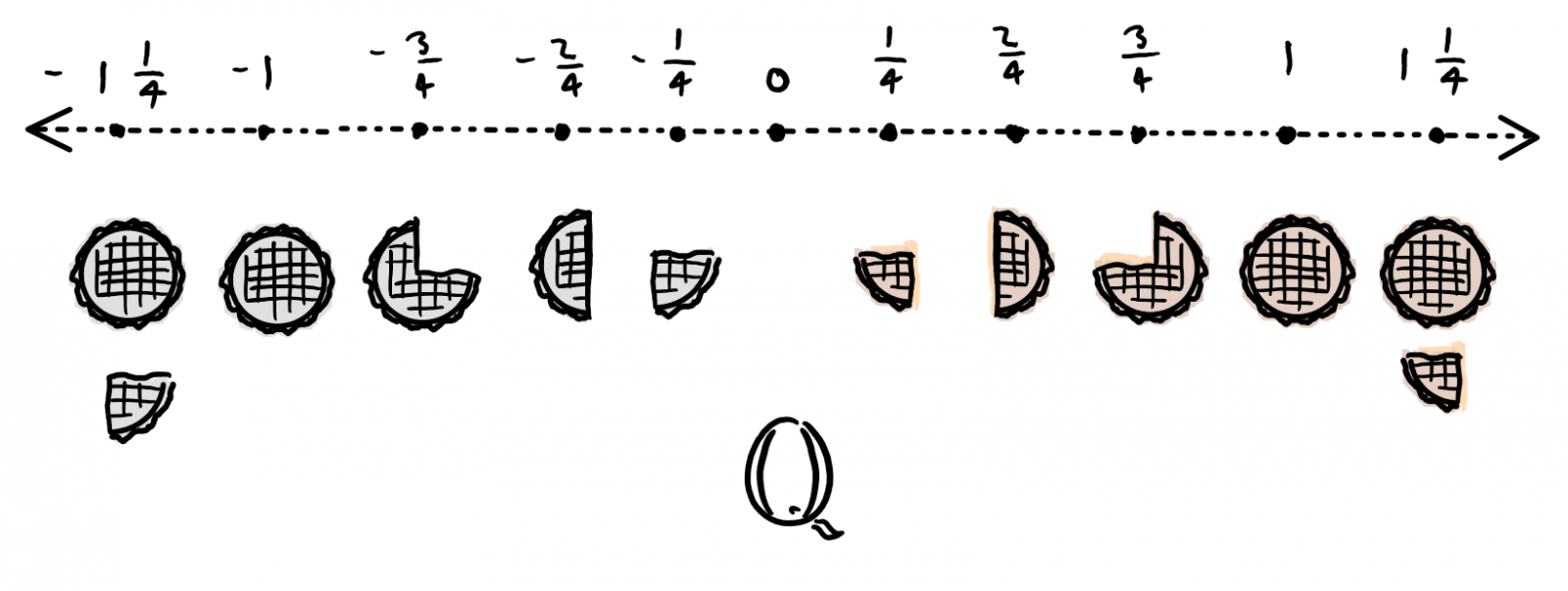 This idea of fractions, or, numbers that aren't quite whole integers, is known as the rational number abstraction. The rational numbers contain all off the integers as well as any finite fractional combinations in between them, and are represented by a double-stroke Q.
This idea of fractions, or, numbers that aren't quite whole integers, is known as the rational number abstraction. The rational numbers contain all off the integers as well as any finite fractional combinations in between them, and are represented by a double-stroke Q. and let us keep cleaving this graphite…
and let us keep cleaving this graphite… …until we've cleaved it so many times, that our pieces are now an incredibly small fraction of a whole. So small, that we can't reasonably describe them with fractions anymore!
…until we've cleaved it so many times, that our pieces are now an incredibly small fraction of a whole. So small, that we can't reasonably describe them with fractions anymore! To measure continuous quantities, we need a further abstraction. The real numbers, represented by , contain all possible base-10 numbers, including all possible radix values. That is to say they contain all numbers, and all possible decimals, from negative infinity to positive infinity. It's impossible to count the real numbers and further, it's impossible to define any "smallest real number"; no matter what number you choose, there will always be one that's closer to zero.
To measure continuous quantities, we need a further abstraction. The real numbers, represented by , contain all possible base-10 numbers, including all possible radix values. That is to say they contain all numbers, and all possible decimals, from negative infinity to positive infinity. It's impossible to count the real numbers and further, it's impossible to define any "smallest real number"; no matter what number you choose, there will always be one that's closer to zero.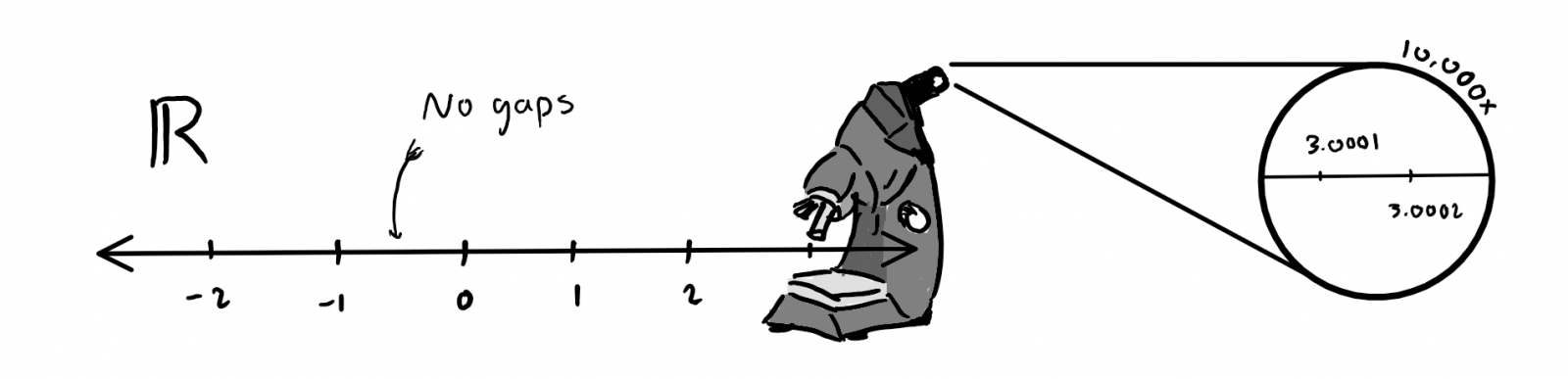 When we think of "numbers", we usually refer to the real numbers.
When we think of "numbers", we usually refer to the real numbers.

Natural Numbers
The counting numbers, or natural numbers, begin at one and increment by one to infinity. Infinity itself is not a number, but rather a concept of "boundless", in so far as it is possible to count upward forever!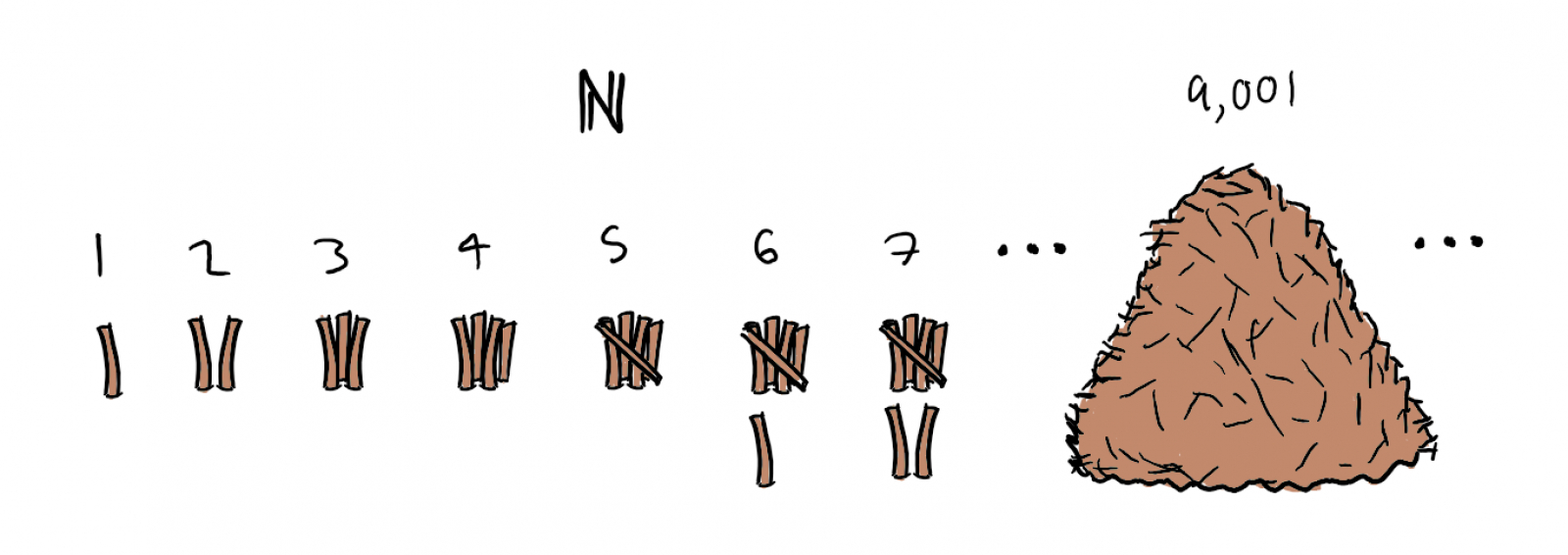
Integers
Now with a concept of a symbolic representation established, it's possible to further abstract this idea into something a bit more useful. What if we wish to describe not only the quantity of apples we own, but on some days, the quantity of apples owed to us by another party? To accomplish that, we’ll need symbols to represent the apples due to us, as well as a symbol to represent the situation in which there are no apples to be had at all.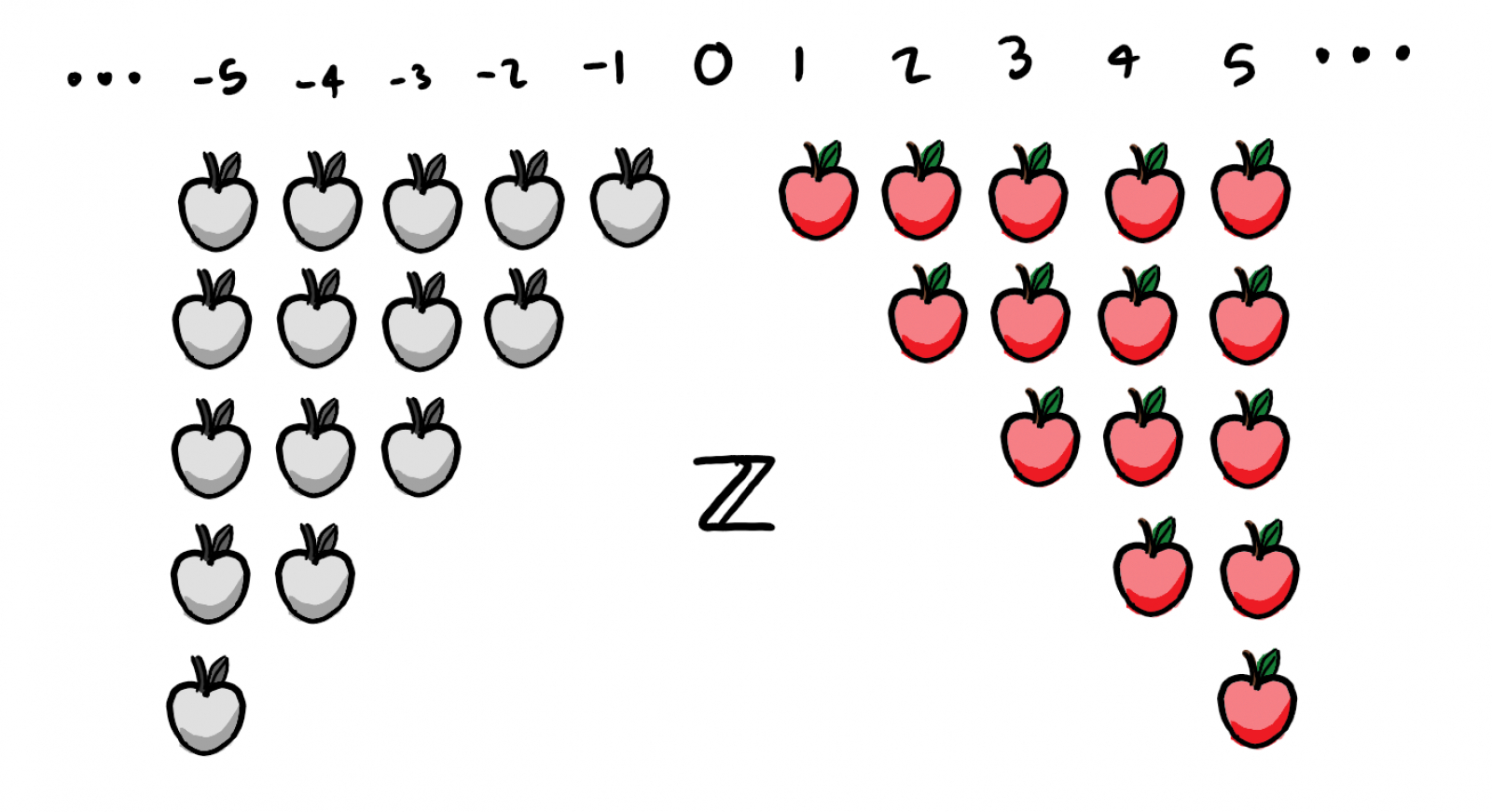
Rational Numbers
Though the integer abstraction serves us well in our apple situation, what if we wished to describe something even more complex? Perhaps, slices of apple pie. It’s possible to divide one pie into an arbitrary number of pieces, and the size of any piece may be easily known by comparing its size to that of a whole pie. If we are tasked with counting pies however, then slices cannot be described by whole numbers. Rather, they are fractions of a whole.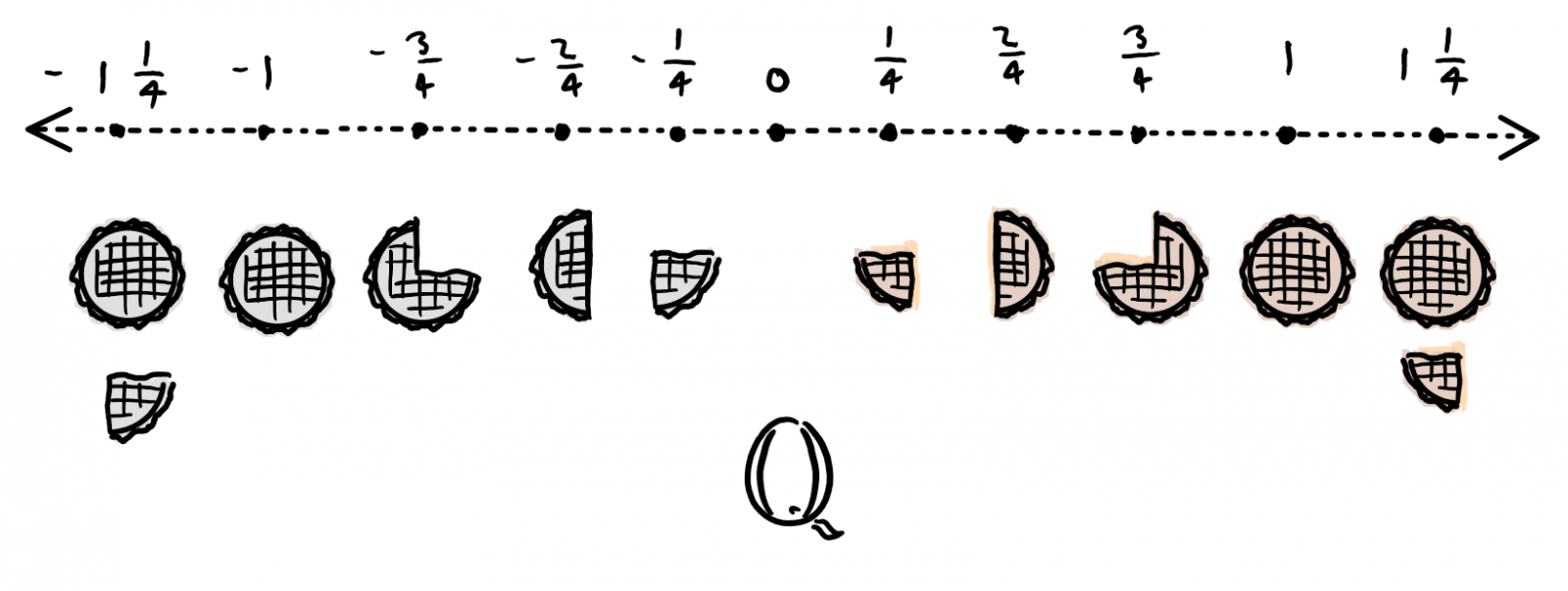
Real Numbers
With fractions established, an important question arises; does the rational number system, contain every possible value there is? Could we, for example use it to measure something continuous, like the distance between two moving points?An interesting way to think about this is to consider the following scenario:Let's take a stick of graphite, and cleave it in two. Let us then cleave it in two again, and again.


